The ICH Q8 core definition of design space is by now somewhat familiar: “The multidimensional combination and interaction of input variables (e.g., material attributes) and process parameters that have been demonstrated to provide assurance of quality” [1]. This definition is ripe for interpretation. The phrase “multidimensional combination and interaction” underscores the need to utilize multivariate analysis and factorial design of experiments (DoE), while the words “input variables (e.g., material attributes) and process parameters” remind us of the importance of measuring the right variables.
However, in presentations and articles discussing design space, not much focus has been given to the key phrase, “assurance of quality”. This does not seem justified, given that guidance documents such as ICH Q8, Q9, Q10, PAT, etc. are inundated with the words “risk” and “risk-based.” For any ICH Q8 design space constructed, surely the core definition of design space begs the question, “How much assurance?” [2]. How do we know if we have a “good” design space if we do not have a method for quantifying “How much assurance?” in a scientifically coherent manner?
The Flaws of Classical MVA
Classical multivariate analysis and DoE methodology fall short of providing convenient tools to allow one to answer the question “How much assurance?” There are two reasons for this. One is that multivariate analysis and DoE have historically focused on making inferences primarily about response means. But simply knowing that the response means of a process meet quality specifications is not sufficient to allow one to conclude that the next batch of drug product will meet specifications. One reason for this is that we always have batch-to-batch variation. Building a design space based upon overlapping mean responses will result in one that is too large, harboring operating conditions with a low probability of meeting all of the quality specifications. Just because each of the process mean quality responses meet specification does not imply that the results of the next batch will do so; there will always be variation about these means.
However, if we can quantify the entire (multivariate) predictive distribution of the process quality responses as a function of “input variables (e.g., material attributes) and process parameters”, then we can compute the probability of a future batch meeting the quality specifications. The multivariate predictive distribution of the process quality responses incorporates all of the information about the means, variation, and correlation structure among the response types.
Another, more technically subtle reason, that classical multivariate analysis and DoE methodology do not provide straightforward tools to construct a proper design space is that, beyond inference about response means, they are oriented towards construction of prediction intervals or regions. For a process with multiple critical quality responses, it is awkward to try to use a classical 95% prediction region (which is not rectangular in shape) to compare against a (rectangular) set of specifications for multiple quality responses. On the other hand, using individual prediction intervals does not take into account the correlation structure among the quality responses. What is needed instead is a “multivariate predictive distribution” for the quality responses. The proportion of this predictive distribution that sits inside of the rectangular set of quality specifications is then simply a quantification of “how much assurance”.
The Stochastic Nature of Our Processes
Complex manufacturing processes are inherently “stochastic processes”. This means that while such process may have underlying mechanistic model relationships between the input factors and process responses, nonetheless such relationships are embedded with random variation. Conceptually, for many complex manufacturing processes, even if “infinitely” accurate measurement devices could be used, such processes would still produce quality responses that vary from batch to batch and possibly within batch. This is why classical multivariate analysis and DoE methodology, which focuses on inference for response means, present an insufficient tool set. This is not to say that such methods are not necessary; indeed they are. However, we need to better understand the multivariate stochastic nature of complex manufacturing processes in order to quantify “how much assurance” relative to an ICH Q8 design space.
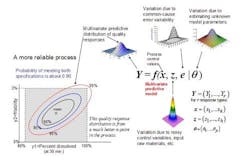
The concept of a multivariate distribution is useful for understanding complex manufacturing processes, with regard to both input variables and response variables. Figure 1 shows a hypothetical illustration of the relationships among various input variables and response variables. Notice that some of the input variables and the response variables are described by multivariate distributions. In Figure 1 we have a model which describes the relationships between the input variables, the common cause process variability and the quality responses. This relationship is captured by the multivariate mathematical function f=(f1,…,fr), which maps various multivariate input variables, x, z, e, θ to the multivariate quality response variable, Y=(Y1,…,Yr). Here, x=(x1,…,xk) lists the controllable process factors (e.g. pressure, temperature, etc.), while z=(z1,…,zh) lists process variables which are noisy, such as input raw materials, process set-point deviations, and possible ambient environmental conditions (e.g. humidity).
The variable e=(e1,…,er) represents the common-cause random variability that is inherent to the process. It is natural that z and e be represented by (multivariate) distributions that capture the mean, variation about the mean, and correlation structure of these random variables. The parameter θ = (θ1,...θp) represents the list of unknown model parameters. While such a list can be thought of as composed of fixed unknown values, for purposes of constructing a predictive distribution, it may be easier to describe the uncertainty associated with these unknown model parameters by a multivariate distribution. The function f then transmits the uncertainty in the variables z, e, and θ to the response variables, Y. In other words, the “input distributions” for z, e, and θ combine to produce the predictive distribution for Y through the process model function f.
The controllable process factors x can then be used to move the distribution of response variables Y to be better situated within the region bounded by the quality specifications. In Figure 1, the rectangular gray region in the lower left is the region bounded by the quality specifications for “percent dissolved” and “friability” for a tablet production process. Here, one can see that the process operating at operating set point x it not reliable because only about 65% of the predictive distribution is within the region carved out by the quality specifications. (The concentric elliptical contours are labelled by the proportion of the predictive distribution inside of each contour.)
In Figure 2, however, one can see that the operating set point x is associated with a much more reliable process since about 90% of the predictive distribution is within the region carved out by the quality specifications. Situations like that in Figure 2 can then be used to create a design space in the following way: A design space (for a process with multiple critical quality responses) can be thought of as the collection of all controllable process factors (x-points) such that the an acceptably high percentage of the (multivariate) predictive distribution of critical quality responses falls within the region outlined by the (multiple) quality specifications.
From Bayesian to Bootstrapping
Viewing Figures 1 and 2 shows that one can get a predictive distribution (for the quality responses in Y) if one has access to the various input distributions, in particular the multivariate distribution representing the uncertainty due to the unknown model parameters. But how can one compute the distribution representing the uncertainty due to the unknown model parameters? One possible approach is to use Bayesian statistics.
The Bayesian statistical paradigm provides a conceptually straightforward way to construct a multivariate statistical distribution for the unknown model parameters associated with a manufacturing process. This statistical distribution for the unknown model parameters is known as the “posterior” distribution by Bayesian statisticians. The resulting distribution for Y (in Figures 1 and 2) is called the posterior predictive distribution. This distribution accounts for uncertainty due to common-cause process variation as well as the uncertainty due to unknown model parameters. It also takes into account the correlation structure among multiple quality response types. In addition, the Bayesian approach also allows for the inclusion of prior information (e.g., from previous pilot plant and laboratory experiments). In fact, use of the posterior predictive distribution is an effective way to do process optimization with multiple responses [3]. An excellent overview of these Bayesian methods is given in the recent book Process Optimization: A Statistical Approach [4]. An application of the Bayesian approach to Design space construction is given by this author in [5].
An alternative approach for obtaining a distribution to represent the uncertainty due to the unknown model parameters involves a concept called “parametric bootstrapping”. This concept is somewhat more transparent than the Bayesian approach. A simple form of the parametric bootstrap approach can be described as follows. First fit your process model to experimental data to estimate the unknown model parameters. Using computer simulation, simulate a new set of (artificial) responses so that you will have new responses similar to the ones obtained from your real experiment. Using the artificial responses, estimate a new set of model parameters. Do this many more times (10,000 say) to obtain many more sets of model parameter estimates. Each of these model parameters (obtained from each artificial data set) will be somewhat different, due to the variability in the data. The collection of all these sets of model parameter estimates forms a bootstrap distribution of the model parameters that expresses their uncertainty. An experiment with a large number of runs (i.e. a lot of information) will tend to have a tighter distribution, expressing the fact that we have only a little uncertainty about the model parameters. But an experiment with only a little information will tend to yield a bootstrap distribution that is more spread out. This is particularly the case, if the common cause variation in the process is also large.
The parametric bootstrap distribution can then be used in place of the Bayesian posterior distribution to enable one to obtain a predictive distribution for the quality responses. This simple parametric bootstrap approach will approximate the Bayesian posterior distribution of model parameters, but it will tend to produce a parameter distribution that is smaller (i.e., a bit too small) than the one obtained using the Bayesian approach. More sophisticated parametric bootstrap approaches are possible [6] which may result in more accurate approximations to the Bayesian posterior distribution of model parameters.
Software Selection
Unfortunately, the DoE software available in many point-and-click statistics packages does not produce multivariate predictive distributions. It therefore does not provide a way to quantify “How much assurance” one can assign to the Design space. So clearly, easy-to-use software is a current bottleneck to allowing experimenters to produce Design spaces based upon multivariate predictive distributions.
However, there are some software packages that consulting statisticians can use to produce approximate predictive distributions. The SAS statistical package has a procedure call PROC MODEL. (It is part of SAS’s econometric suite of procedures.) This procedure will analyze multivariate response regression models. It has a Monte Carlo option which will produce simulations that allow one to sample from a predictive distribution. This is useful if the process you have can be modeled using PROC MODEL.
The R statistical programming language has functions which will allow the user to do a Bayesian analysis for certain multivariate response regression models. In addition R has a boot function which will allow the user (in conjunction with other R statistical functions) to perform a parametric bootstrap analysis, which can eventually be incorporated into an R program for creating an approximate multivariate predictive distribution. In any case, the SAS and R software does require some statistical sophistication in order to create the appropriate programming steps. Easier to use point-and-click software is still very much needed to lower the computational hurdles for generating multivariate predictive distributions needed for ICH Q8 design space development.
Putting It All Together
Viewing the multivariate world from our limited three-dimensional perspective is often a challenge. This is no different for a design space involving multiple controllable factors. For the design space definition above, it is convenient to use a probability function, P(x), which assigns a probability (i.e., reliability measure) to each set of process operating conditions, denoted by x = (x1,…, xk). Here, P(x) is the probability that all of the critical quality responses simultaneously meet their specification limits. As stated previously, this probability can be thought of as the proportion of the predictive distribution contained within the region bounded by the quality specifications. The design space is then the set of all x such that P(x) is at least some acceptable reliability value. One can then plot P(x) vs. x to view the design space, provided that the dimension of x (i.e., k) is not too large. A simplified example discussed in [5] and [7] is briefly described below.
In an early phase synthetic chemistry study, a prototype design space using a predictive distribution was created for an active pharmaceutical ingredient (API). The (four) quality responses considered were: “% starting material isomer” (<0.15%), “% product isomer” (<2%), “% of impurity #1” (<3.5%), and “% API purity” (>95%). Four controllable experimental factors (x = (x1,…, x4)) were used in a DoE to model how they (simultaneously) influenced the four quality responses. These factors were x1=temperature (oC), x2=pressure (psi), x3= catalyst loading (eq.), and x4=reaction time (hrs).
A Bayesian statistical analysis was used to construct the multivariate predictive distribution for the four quality responses. For the above quality specifications (in parentheses), and for various x-points, the proportion of the multivariate predictive distribution inside the specification region was computed using many Monte Carlo simulations. In other words, for each x-point the corresponding P(x) value was computed. A multipanel contour plot of P(x) vs. the four experimental factors is shown in Figure 3 below. The white regions indicate the regions of larger reliability for simultaneously meeting all of the process specifications. Although these absolute reliability levels are less than ideal, this example is useful for illustration purposes.
As it turned out, the “optimal” factor-level configurations were such that the associated proportions of the predictive distributions were only about 60% to 70% inside of the quality specification region. Part of the reason for this is that the “input” distributions corresponding to the “unknown model parameters” and the “common cause variation” were too large. A more detailed analysis of this data, conducted in [7], indicates that if a larger experimental design had been used and the process variation reduced by 30%, the more reliable factor conditions would be associated with reliability measures that were to the 95% level and beyond. This shows the importance of reducing the variation for as many of the process “input” distributions (of the kind shown in Figures 1 and 2) as is possible.
In the case where the dimension of x is not small, a (read-only) sortable spreadsheet could be used to make informed movements within such a design space [5]. While the spreadsheet approach does not provide a high-level (i.e., bird’s eye) view of the design space (as in Figure 3), it does show (locally) how P(x) changes as various controllable factors are changed. In theory, it may also be possible to utilize mathematical optimization routines applied to P(x) to move optimally within a design space whose dimension is not small.
Developing Design Spaces Based Upon Predictive Distributions: A Summary
Emphasize efficient experimental designs, particularly for multiple unit operations. For design space construction, clearly it is desirable to have good data that can be efficiently collected. As such, good experimental design and planning is critical. It is particularly useful to have good data that can be efficiently collected across various unit operations in a multi-step process. The performance of one unit operation may depend upon various multiple aspects of previous unit operations. When viewed as a whole, a process may have a variety of interacting variables that span its unit operations. This is an aspect of process optimization and design space construction that requires more research by statisticians and their clients (chemical engineers, chemometricians, pharmaceutical scientists, etc.). Some work has been done [8] but more is needed. Poor experimental designs can be costly and possibly lead to biases and/or too much uncertainty about unknown model parameters. This is not helpful for developing a good multivariate predictive distribution with which to construct a design space.
Depend upon easy-to-use statistical software for multivariate predictive distributions. As mentioned previously in this article, the availability of easy-to-use statistical software for creating multivariate predictive distributions is a key bottleneck for the development of design spaces that quantify “how much assurance” can be associated with meeting quality specifications. More broadly, it has been shown recently that multivariate predictive distributions can be very useful for process optimization involving multiple responses [3], [4]. Monte Carlo simulation software applications such as @Risk and Crystal Ball provide point-and-click software for process simulation. However, a key issue that still remains involves producing a multivariate distribution that reflects the uncertainty of unknown model parameters associated with a process. Producing such a distribution is not always statistically simple.
The Bayesian approach provides a unifying paradigm, but the computational issues do require careful assessment of model and distributional assumptions, and in many cases, careful judgement involving convergence of algorithms. The parametric bootstrap approach is more transparent but may produce design spaces that are a bit too large, unless certain technical refinements are brought to bear. Nonetheless, the statistical methods exist to produce good multivariate distributions that represent the uncertainty of unknown model parameters. As always, modeling and inference need to be done with care, using data from appropriately designed experiments.
Use computer simulation to better understand reliability and risk assessments for complex processes. If one can state that they understand a process quantitatively, even a stochastic process, then one should expect that they can simulate such a process reasonably well. Given that many pharmaceutical processes may involve a series of complex unit operations, computer simulation may prove to be helpful for understanding how various process factors and conditions combine to influence multivariate quality responses. With proper care, computer simulation may help process engineers and scientists to better understand the multivariate nature of their multi-step manufacturing procedures. Of course, experimental validation of computer simulation findings with real data may still be needed. In addition, process risk assessments based largely upon judgement (e.g., through tools such as FMEA) can be enhanced through the use of better quantitative methods such as probability measures [9] (e.g., obtained through computer simulations). The issue of ICH Q8 design space provides a further incentive to utilize and enhance such computer simulation tools.
Have a clear understanding of the processes involved and lurking risks, not just the blind use of mathematical models. We must always keep in mind that our statistical predictions, such as multivariate predictive distributions, are based upon mathematical models that are approximations to the real world environment. How much assurance we can accurately attribute to a design space will be influenced by the predictive distribution, and all of the modeling and input information (e.g. input distributions) that went into developing it. Generally speaking, of course, all decisions and risk measurements based upon statistical methods are influenced to varying degrees by what mathematical modeling assumptions are used, quantifications of design space assurance are fundamentally no different.
However, seemingly good predictive modeling (along with accurate statistical computation) may not be sufficient to provide a design space with long term, high-level assurance of meeting quality specifications. The issue of process robustness is also important, not only for design space construction but in other areas of QbD as well. This issue has many facets and I believe it needs to be given more emphasis in pharmaceutical product development and manufacturing. So as not to go too far on a tangent, I will only briefly summarize some of the issues involved.
In quality engineering, making a process robust to noisy input variables is known as “robust parameter design” (RPD). The Japanese industrial engineer Genichi Taguchi pioneered this approach to quality improvement. The basic idea is to configure the controllable (i.e., non-noisy) process factors in such as way to dampen the influence of the noise process variables (e.g., raw material attributes or temperature/pressure fluctuations in the process). A convenient aspect of the predictive distribution approach to design space, and process optimization in general, is that it provides a technically and computationally straightforward way to do RPD. We simply simulate the nose variable distribution (shown in Figures 1 and 2) and then configure the controllable factors (x-points) to increase the probability of meeting the quality specifications. If the controllable factors are able to noticeably dampen down the influence of the noise variables, typically the probability that the quality responses will meet specifications will increase (assuming that the mean responses meet their specifications). See [4], [5], and [10] for RPD examples involving multivariate predictive distributions.
Less well known, however, are two more subtle issues that can cause problems with predictive distributions. These are lurking variables and heavy-tailed distributions. Process engineers and scientists need to brainstorm and test various possibilities for a change in the process or its inputs that could increase the risk that the predictive distribution is overly optimistic or is not stable over time.
Some predictive distributions may have what are called “heavy tails”. (The degree of “heavy tailedness” is called kurtosis by statisticians.) We need to be careful with such distributions as they are more likely to suddenly produce values far from the center of the distribution, than for a normal (i.e., Gaussian) distribution.
If the process can be simulated on a computer, sensitivity analyses can be done to assess the effect of various shocks to the system or changes to the input or predictive distributions, such as heavier tails. An interesting overview of these two issues and of how quality and risk combine can be found in [11].
In conclusion, the ability to understand randomness and think stochastically is important as multivariate random variation pervades all complex production processes. Given that we are forced to deal with randomness (in multivariate form, no less), Monte Carlo simulation has become a useful way to gain some insight into the combined effects of controllable and random effects present in a complex production process. (Interested readers may want to visit The American Society for Quality’s web site on Probabilistic Technology available at http://www.asq.org/communities/probabilistic-technology/index.html). Computer simulation can help our intuition for understanding stochastic processes. Such intuition in humans is not always on the mark. We can all be fooled by randomness. See for example the book by Taleb [12].
About the Author
John Peterson is a Director in the Research Statistics Unit of the Drug Development Sciences Department at GlaxoSmithKline Pharmaceuticals, R&D. John’s research interests include applications of response surface methodology to drug discovery and development. He is an elected Fellow of the American Statistical Association. He can be reached at [email protected] or at (610) 917-6242.
References
1. ICH (2005). “ICH Harmonized Tripartite Guideline: Pharmaceutical Development, Q8.”
2. Peterson, J. J. Snee, R. D., McAllister, P.R., Schofield, T. L., and Carella, A. J., (2009) “Statistics in the Pharmaceutical Development and Manufacturing” (with discussion), Journal of Quality Technology, 41, 111-147.
3. Peterson, J. J. (2004), “A Posterior Predictive Approach to Multiple Response Surface Optimization”, Journal of Quality Technology, 36, 139-153.
4. Del Castillo, E. (2007), Process Optimization: A Statistical Approach, Springer, N.Y.
5. Peterson, J. J. (2008), "A Bayesian Approach to the ICH Q8 Definition of Design Space", Journal of Biopharmaceutical Statistics, 18, 959-975.
6. Davison, C. and Hinkley, D.V. (1997), Bootstrap Methods and Their Application, Cambridge University Press, Cambridge, UK.
7. Stockdale, G. W. and Cheng, A. (2009), “Finding Design Space and a Reliable Operating Region using a Multivariate Bayesian Approach with Experimental Design”, Quality Technology and Quantitative Management, (to appear).
8. Perry, L. A., Montgomergy, D.C., and Fowler, J. W. (2002), “Partition Experimental Designs for Sequential Processes: Part II - Second Order Models”, Quality and Reliability Engineering International, 18, 373-382.
9. Claycamp, H. G. (2008). "Room for Probability in ICH Q9: Quality Risk Management", Institute of Validation Technology conference: Pharmaceutical Statistics 2008 Confronting Controversy, March 18-19, Arlington, VA
10. Miro-Quesada, G., del Castillo, E., and Peterson, J.J., (2004) "A Bayesian Approach for Multiple Response Surface Optimization in the Presence of Noise Variables", Journal of Applied Statistics, 31, 251-270
11. Kenett, Ron S and Tapiero, Charles S. (2009),”Quality, Risk and the Taleb Quadrants” presented at the IBM Quality & Productivity Research Conference, June 3rd, 2009. Available at SSRN: http://ssrn.com/abstract=1433490
12. Taleb, Nassim (2008) Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets, Random House, New York.