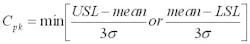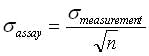Understanding Variability, its Sources and its Impact on the Pharma Supply Chain
A pharmaceutical company operating in the U.S. had encountered frequent release failures of its top selling product. In addition, it had set up a fairly common stability limit (1), which triggered investigations when a stability point differed by more than 5% from its previous measurement. As a result:
- This organization lost several million dollars in the profit that this product was supposed to generate;
- the company experienced several supply chain interruptions, which complicated its relationships with some of its main customers; and
- there were frequent inconclusive stability failure investigations, all of which consumed funds, time and organizational resources.
Management assembled a cross-disciplinary team with the relevant functional departments. I was hired to manage this team and provide quality engineering skills to the organization. Quality engineering is the science of understanding and controlling variation.
Understanding the fundamentals of variation (2, 3)
In a given specification, the total observed variability is the sum of the variability of the assay plus the variability of the process. Mathematically, this can be expressed as:
σ2observed = σ2process + σ2assay
where σ2observed is the observed variance, σ2process is the variance of the process, and σ2assay is the variance of the assay.
The variance of the assay is given by:
σ2assay = σ2repeatability + σ2reproducibility
where σ2repeatability is the precision, or the variance obtained when the same assay is performed by the same analyst, in the same equipment, during consecutive measurements, during the same day. σ2repeatability is the variation between different analysts performing the same assay, in the same equipment, at different days. Both of these parameters are normally determined as part of the assay validation.
It is good practice to set the release specification range at a minimum of 8 σs of the observed variance. The measurement error is six times σ2assay and it should be less than 10% of the specification range. In addition, it is recommended that the ratio of the assay to the observed variance be less than 10%.
σ2assay can be reduced by increasing the number of measurements by using the central limit theorem of statistics, which states that in any population, the variance of means of samples from that population will be the total population variance divided by thewhere n is the number of measurements.
Note that, when the sample size increases, an assay will produce means closer to the true mean, and the spread of the assay results will be narrower.
The capability of a process to meet its specifications can be measured with a term called process capability, which in mathematical terms is expressed as:
where USL and LSL are the upper and lower spec limits, respectively.
σ is the observed standard deviation (from the process and from the assay).
The higher the Cpk values the better. A Cpk of 1 means that the process is barely meeting its specifications and there is no room for variability beyond random variation. A Cpk below 1 means the process is not meeting its specifications, and that out of spec results will be expected. A Cpk above 1 indicates that the process has room for some variability beyond random variation.
Solving the problem of release failures
Release data from approximately 30 lots was collected to calculate the process average and the observed variability. This allowed the calculations of the Cpks with the old specifications. This product has several actives, hence one Cpk per active was calculated. Not surprisingly, several of the Cpks were below 1, which indicated that the specifications were tighter than the normal and random observed variation from both the assays and the process. The solution was then to increase specification ranges of the actives with the lowest Cpks.
The definition of process capability given before suggests two ways to increase the Cpk. One could increase the range of the specifications (LSL and USL), or one could reduce the observed variance. The first option is preferred because it is cheaper and faster. Sometimes there are market- or customer-related limitations on how wide the specification ranges need to be. For example, there are some toxic drugs for which the nurses must know the drug concentration within very narrow ranges to be able to give exact doses to the patients. Or, medical reasons could dictate that drug doses do not exceed certain limits. That was not the case with this product. Therefore, with the approval of the organization's Medical Affairs department, the specification ranges were increased to +/- four standard deviations from the process averages. By definition, this increased the Cpks to 1.33.
The option to increase Cpk through reduction in the observed variability is far more complicated, lengthy and expensive. Assay variability can be calculated from the assay validation reports. Observed variance can be calculated from the release data. Then, from the first formula provided in this article, the process variance can be deducted as the difference between the observed variance and the assay variance. Depending on which is one is relatively bigger, efforts could then be oriented toward reducing either the assay or the process variances.
In this product, the assay variances were significantly larger than the process variances. Therefore, if the option to increase capability through variance reduction had been pursued, it would have meant higher sample sizes (per the above, the observed assay variance is reduced when the sample size increases), or further assay development to identify and eliminate or control assay variation factors.
After the new release limits were suggested, several out-of-specification release results from the old limits were encountered. They were all within the new specification limits, which increased the confidence in the new limits.
Nevertheless, there was the question of what to do with those release failures because the new specification limits required prior approval changes and could not be implemented until approval from the FDA was obtained, which would take months.
Understanding variation helped release those lots and this company saved millions by being able to use those lots, and by not having to put any of them on long-term stability at a cost of $62,000 per lot. Here is how.
The rewards of understanding variation
Assays of multiple actives are very expensive. As a result, only one sample per assay is tested for release. Given that it was demonstrated that the assay variabilities were significant, when only one sample is tested one never knows from which part of the normal curve that measurement comes. Hence, averages are better estimators of the true concentrations of the actives in the lots.
A comparison of the assays' variabilities with the old specification ranges demonstrated that seven additional independent samples per active needed to be tested to meet the requirement that six times the assay standard deviation should consume less than 10% of the specification range. Those additional tests were performed and the averages of those samples and the failing results were used instead as estimators of the true concentrations of the actives in those lots. Fortunately, all averages fell within the old specification limits and hence, those lots were released.
It is important to point out that these actions did not contradict FDA guidelines on retests. In cases like this where it is proven that the assays' variabilities are significant, it is statistically defensible to release a lot based on averages falling within the specification limits, even if some of the measurements used in the calculation of those averages fell outside the specifications (4).
Furthermore, this is in agreement with the FDA guideline on investigating out-of-specification test results, which states that (5): If the samples can be assumed to be homogeneous (i.e., an individual sample preparation designed to be homogeneous), using averages can provide a more accurate result. In the case of microbiological assays, the USP prefers the averages because of the innate variability of the biological test system. The product is a liquid, the samples are homogeneous and the actives are well dissolved. Most important, although the assays are HPLC-based and not microbiological, the demonstrated assays' variabilities parallel the USP and FDA allowances of the use of averages in microbiological assays, because in these cases, averages are better predictors and more reliable than any of the individual results.
These actions are also in line with the Barr decision (6) because there was a limit at which retesting stopped (seven additional samples) and there was a clear decision on what to do before the retests: release the lots if averages fall within the old specifications, or reject the lots if the averages fall outside those ranges.
Additional confidence in this decision was gained by using three independent statistical tests to prove by three different methods that there were not statistically meaningful differences between the lots with all passing results and the lots in which some of the results had fallen outside the old specification limits. Those tests were the probabilities that, given the assays' variabilities and the averages, individual results will fall outside the old specs; analysis of variance (ANOVA); and t-test checks, which test the hypothesis that the averages come from the same populations. The use of hypothesis testing and calculation of normal probabilities are outside the scope of this article. Suffice to say those three independent tests confirmed the validity of the decision to use the lots.
Solving the problem of stability failures
The establishment of statistically defensible stability limits is a fairly complicated topic. Those limits have to be calculated on a case-by-case basis, based on each situation and set of data (7).
This organization had set up stability alerts limits when a stability result differed by more than 5% from a previous value. This is not statistically defensible (1) and it triggered automatic investigations, which were all inconclusive. The calculation of the assay variability with data from the assay validation reports demonstrated that this 5% limit did not make sense because the assay variations of several of the actives were much higher than 5%. As a result, even if the stability concentrations did not change over time, measuring of the same sample by different analysts over different days generated the results with a range of six times the assays standard deviations, many of which were higher than 5%.
Hence, eliminating this 5% limit will save thousands of dollars in retests and investigations.
About the Author
Fernando Portes, MEng, MPS, MBA, PMP, CQE, is a Principal Project Manager for Best Project Management (www.bestpjm.com), which provides hands-on project management services in the U.S. and internationally. He has 17 years of experience in the pharmaceutical and medical device industries, and has managed technology transfer, validation, capital, process improvement, start-up, compliance, Six Sigma, supply chain and procurement projects for 14 years, mostly at Fortune 100 organizations. Portes has M.Eng. and MPS degrees from Cornell University, and an MBA from Catholic University, Santo Domingo. He also has B.Eng. (Chemical Engineering, Magna Cum Laude) and B.S. (Chemistry, Magna Cum Laude) degrees from the Autonomous University of Santo Domingo.
Portes is also a Project Management Professional (PMP), a Certified Quality Engineer (CQE), and a member of PMI. He is also an Affiliate Professor and teaches graduate-level project management at Stevens Institute of Technology (Hoboken, N.J.). He can be reached at 201-617-9240, or at [email protected].
References
1. Identification of Out of Trend Stability Results. A Review of the Potential Regulatory Issue and Various Approaches. PhRMA CMC Statistics and Stability Expert Teams. Pharmaceutical Technology. April 2003.
2. The Quality Engineer Primer. Bill Wortman. Quality Council of Indiana. 1991. Pages MC26-MC30.
3. Quality Control Handbook. J.M. Juran and Fran M. Gryna. McGraw-Hill, 4th Edition, 1986. Pages 18.63-18.69.
4. Identification of Out of Specification Results. Alex M. Hoinowski, Sol Motola, Richard J. Davis, James V. McArdle. Pharmaceutical Technology. January 2002.
5. Investigating Out of Specification Spec Results for Pharmaceutical Production. Food and Drug Administration. Center for Drug Evaluation and Research (CDER). September 1988.
6. USA Versus Barr Laboratories, Civil Action Number 92-1744. February 1993.
7. Identification of Out of Trend Stability Results. Part II. PhRMA CMC Statistics and Stability Expert Teams. Pharmaceutical Technology. October 2005.