There is a perceived market need, dictated by the FDA, to maintain the accuracy of sensors that are defined as current Good Manufacturing Practices (cGMP) values in a validated pharmaceutical process. Today, this is achieved by maintaining a costly routine calibration protocol.
In Part 1 of this article (“Don’t Drift Out of Control,” October 2008), I introduced an aggressive technique to shift from routine preventive maintenance methodology (i.e., to calibrate an instrument every six months regardless of past experience) to a predictive maintenance methodology using pairs of instruments and performing a statistical analysis of their behavior. When the statistical analysis recognizes that at least one of the instruments is beginning to drift away from its paired instrument, an alarm message can be sent to the metrology department to schedule a calibration of both instruments.
The upside of this technique is that it will detect drifting instruments in real time, thus eliminating the need for non-value-added routine calibrations that can be 50% of the metrology department’s budget, and will provide immediate notification of a developing calibration problem before the instrument and the related product quality parameter goes out of specification.
The downside is the capital expense to add a second instrument to any validated instrument where you elect to adapt this technique. At first blush this will appear to be a belt-and-suspenders solution, but it is necessary in order to detect common cause failures that will have to be addressed if you elect to depend on a predictive rather than a preventive maintenance strategy. However, the economic justification is certainly there for instruments where product quality is a major issue or where the cost of a routine calibration is very expensive, such as in a hazardous area.
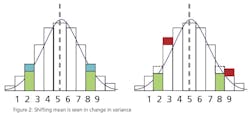
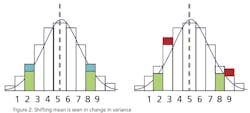
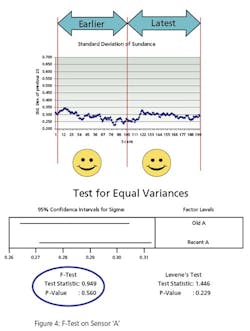
This leads to a more practical question: What can a statistical analysis provide without the cost of the additional instruments? The answer may surprise you. There is hidden data in an instrument’s signal that can provide an indication that an instrument’s behavior has changed. This phenomenon can be used to predict the need for calibration and therefore capture the second benefit of detecting a drifting instrument before it affects quality. Since it’s a single instrument solution, it is unlikely to totally eliminate periodic calibrations, but it can provide quantifiable data to justify a longer interval between calibrations. The hidden data is the variance in the instrument’s signal.
Calibration Basics
Let us begin by establishing a base level of understanding of instrumentation calibration.
Precise, dependable process values are vital to an optimum control scheme and, in some cases, they are mandated by compliance regulation. Precision starts with the selection and installation of the analog sensor while the integrity of the reported process value is maintained by routine calibration throughout the life of the instrument.
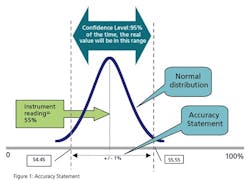
When you specify a general purpose instrument, it has a stated accuracy—for example, +/- 1% of actual reading. In the fine print, that means that the vendor states that the reading of the instrument will be within 1% of reality 95% of the time (certainty). Figure 1 illustrates this concept.
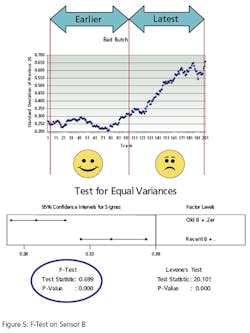
The second test, Figure 5, conducts the same test on a different instrument. It compares the variance of instrument B’s oldest 500 values to its most recent 500 reading. Instrument B has bias superimposed on its last 500 values to simulate error. The F-Test p-Value of .00 (>.05) indicates that the variances are “different”.