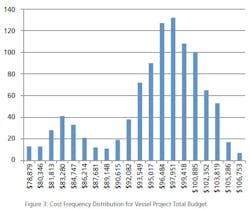
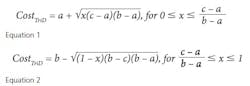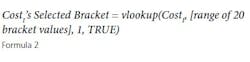Estimating capital project budgets can be a tricky business. There are many factors to include as inputs to the budget: vendor quotes, capital labor, permits, third- party inspections, expenditure data from previous projects, material escalation… the list goes on and on. Unfortunately, each input can itself be an estimate, and each input can present cost uncertainty risks. Because it is impossible to calculate a precise, infallible budget (owing to the nature of project risk and cost uncertainty), numerical analysis is a good option for arriving at a solution. In the case of predicting capital budgets, the Monte Carlo Simulation (MCS) is the numerical method of choice.
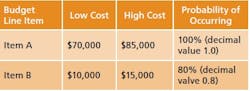
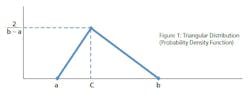
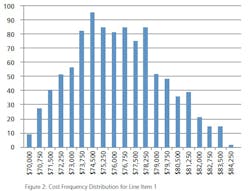
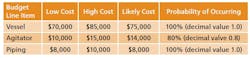
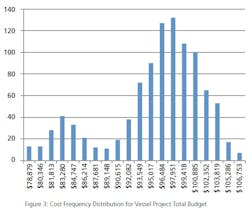
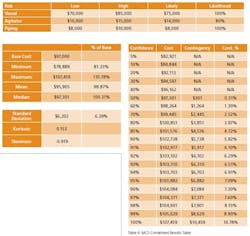
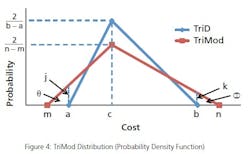
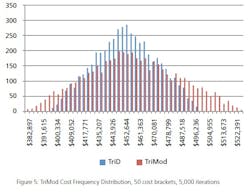
What is a MCS? In terms of project cost risk, the MCS is a tool for calculating the statistical likelihood of exceeding a base budget by a given value. The goal is to assign a statistically-derived dollar value to the various risks associated with the project. The MCS calculates budget values and likelihoods based on two key inputs for each budget line item: 1) the forecasted cost distribution for the expenditure, and 2) the chance of incurring the expenditure.For example, Item A should cost between $70,000 and $85,000, and there is a 100% of incurring the cost; Item B should cost between $10,000 and $15,000, but there is only an 80% chance of incurring the cost. (Table 1).References:
Kots, Samuel, and Johan Rene van Dorp. Beyond Beta – Other Continuous Families of Distributions with Bounded Support and Applications. Singapore: World Scientific Publishing Co, 2004. Print.
About the Author:
Keith Melchiors is currently a process engineer at Biogen Idec in Research Triangle Park, North Carolina. During the writing of this article, he was senior process engineer with Integrated Process Technologies in Cary, N.C. Keith earned his B.S. ChE from Purdue University in 2002, and has 10 years experience in biopharmaceutical process design and capital project execution.
Related article:
Quantifying Breakeven Point with Contingencies