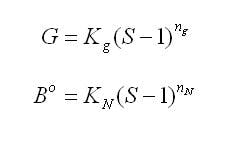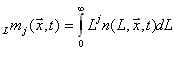• Magazine
  • ENEWS
  • SUBSCRIBE
  • WEBINARS
  • PODCASTS
  • EBOOKS
    1. Production
    2. Automation & Control

    Controlling Crystallization through Modeling

    Aug. 5, 2005
    CFD modeling and particle population control are key to improving processes and product quality at the crystallizer, and further downstream.
    1660255633988 Pm0507 Crystallization Fig2
    Controlling a product’s crystal size distribution (CSD) is one of the key challenges in drug manufacturing. CSD control is critical to successful crystallizer operation and to product quality and purity, as CSD often impacts downstream processing such as filtration, centrifugation and milling. Size distribution also affects the rate at which a powdered material dissolves in the body. Thus, greater control of CSD leads to better control of the release rate of active ingredients.In spite of its importance, CSD control is not well understood. Part of the complexity is that size distribution varies in space and time in a crystallizer due to non-ideal flow patterns and heat transfer. Furthermore, it is dependent upon solution thermodynamics and crystallization phenomena such as nucleation, growth, aggregation and breakage. A better understanding of CSD can be gained through detailed modeling such as computational fluid dynamics, or CFD, which studies the effect of fluid mechanics and non-ideal mixing on processes (see A CFD Primer, below). CFD is an established technology that can predict the fluid flow and mixing characteristics in a wide range of applications. It can also facilitate product scale-up through better understanding of the interactive effects of mixing, fluid mechanics, solid and liquid chemical-physical properties, and the overall supersaturation profile. Such a science-based approach falls directly in line with FDA’s process analytical technology (PAT) initiative.Despite their importance, detailed models have not been used to their full potential in pharmaceutical crystallization. Simple models such as Mixed-Suspension Mixed-Product Removal (MSMPR) models have been more popular but have limited usefulness. For instance, they assume the crystallizer is well-mixed and neglect hydrodynamic effects. Nevertheless, these simple models have been used extensively in designing crystallizers and, as a result, current designs are extremely conservative and are not optimized for operation or yield.The problem is made worse by the fact that, in pharmaceutical crystallization, new drugs are typically made in existing stirred tanks that allow for limited changes to operation profiles and no design modifications. The lack of understanding of the flow characteristics and crystallization kinetics within these tanks makes process development and scale-up difficult and time consuming.Mixing analyses definedMixing analyses based on CFD can provide significant insight into the crystallization process. For example, in antisolvent addition, key decisions about the feed location, feed pipe diameter and feed rates can be made by understanding the local flow field and local mixing characteristics. The mixing analyses can include macromixing, mesomixing and micromixing effects.Macromixing effects include prediction of blend times, power numbers, turbulence quantities and shear quantities. During scale-up or a scale-down analysis, using these predictions can help in deciding impeller speeds (in rpm), locations and types. Since most manufacturers do not have the flexibility to change impellers or purchase new equipment, it is important to choose the right reactor vessel from those available within the production facility. An example of a mixing time analysis is shown in Figure 1, below.
    pm0507_crystallization_fig1

    Figure 1. Left: Dimensionless tracer concentration monitored at different locations as a function of time. Right: Velocity contours in tank showing regions of high velocity (red) and regions of low velocity (blue).

    pm0507_crystallization_fig2
    Figure 2. Velocity contours in a glass-lined crystallizer vessel. Antisolvent addition through a dip-tube and the feed path is shown through fluid-packets represented by spheres and colored by residence time.

    Mesomixing helps in understanding local turbulence due to the addition of antisolvent or reactant. This is typically important for fast additions. Figure 2 (at right) shows an example of antisolvent addition and its path through a semi-batch crystallization process.For slow additions, micromixing effects become important. Micromixing is mixing at a molecular scale and affects the course of the crystallization and most definitely affects particle size and morphology. The effects of micromixing can be incorporated into CFD through additional transport equations and help predict supersaturation history more accurately.Particle population controlPopulation balance can be incorporated into CFD models to predict crystal size distribution. Fluid flow occurs in conjunction with evolutionary processes such as nucleation and growth, producing the crystalline phase. The population balance equation accounts for various ways in which particles of a specific state can form, migrate to another state or disappear from the system. Typically, these ways are nucleation, growth, dissolution, aggregation and breakage. Together, these processes are called crystallization phenomena.The population balance equation is coupled with flow, energy and species (mass balance) equations through convective terms and local values such as velocity, turbulence and temperature in different parts of the crystallizer. The population is usually described by the number density of particles, and the usual conservation law can be written for the number density, which includes birth and death terms due to the above processes. There are two approaches of solving population balance equations in CFD: the Discrete Method and the Quadrature Method of Moments (see Trust Your MOM (and DM and QMOM), below). In the Discrete Method, the particle population is discretized into a finite number of size intervals. This approach can be computationally expensive for crystallization applications as the particle size varies widely. Nucleation occurs in the smallest of size scales, typically 10 to 20 nm. Aggregation and growth can yield larger particles and the size distribution can span three to five orders of magnitude.
    pm0507_crystallization_betterfig3
    Figure 3. Crystal Size Distribution averaged over the entire crystallizer volume.

    Examples of QMOMThe Quadrature Method of Moments (QMOM) is an attractive approach, as it allows modeling arbitrary kinetics involving nucleation, growth, aggregation and breakage. In addition, one can recover the crystal size distribution using available numerical techniques to invert the moments.Consider a batch crystallization problem with a typical drug dissolved in a solvent. The mixture was initiated at a temperature of 353 K and the walls were cooled at 298 K. The supersaturation ratio, S, is defined as the ratio of concentration of drug in solution to its solubility. A solubility curve that exhibits a linear dependency on temperature in the operating range is assumed. The growth (G) and nucleation (Bο) kinetics are based on power-law kinetics as:
    pm0507_crystallization_powerlawkineticsfig

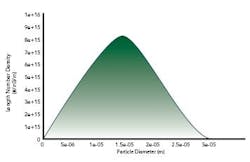
    The analysis predicted the moments of the crystal size distribution. From the moments, the crystal size distribution at final state was obtained, as shown in Figure 3, above.In summary, crystallization process understanding can be gained through systematic modeling studies starting from mixing analyses with CFD. In a staged modeling approach, it is possible to study mixing at different scales such as macromixing, mesomixing and micromixing. If knowledge of crystallization kinetics is available, the models can be expanded to include kinetics to predict crystal size distribution and related parameters.About the AuthorsDr. Dhanasekharan is a consulting team leader at Fluent, Inc. (Lebanon, N.H.). His team focuses on providing engineering solutions to the healthcare industry. He has several years engineering experience in the field of fluid flow and related transport. He specializes in particulate flows and technology, specifically in pharmaceutical crystallization. He can be reached at [email protected].Dr. Ring is professor and past chair of the Department of Chemical Engineering at the University of Utah. He received his Ph.D. in chemical engineering from Cambridge University, and has also held faculty positions at Massachusetts Institute of Technology and the Swiss Federal Institute of Technology in Lausanne. His latest research interests include: the effects of additives on the nucleation and growth of crystals, the fundamentals of nucleation to produce nanoparticles, population balance modeling using CFD and the fabrication of sensors from thin film ceramics. He can be reached at [email protected].


    A CFD Primer

    Computational fluid dynamics (CFD) uses numerical methods to solve fundamental conservation (transport) equations for fluid flow, heat and mass transfer and related phenomena such as population balances. The approach builds a 3D model of any unit operation and divides the fluid flow region into a large number of control volumes. On each of these control volumes, the basic conservation of mass, momentum and heat equations is solved and thus a global conservation of these quantities is automatically satisfied. This allows CFD to work on any arbitrary geometry, including moving parts.

    The number of control volumes can be as many as several million, more than enough to provide a fine spatial resolution of the flow features and related processes that occur within the unit operation. The basic benefit of this modeling approach is an increased understanding and insight into the processes taking place in the unit operation.

    A CFD analysis yields values for fluid velocity, fluid temperature and fluid concentration at every control volume throughout the solution domain. As might be expected, a fine mesh or grid of control volumes provides a more accurate, but also a more expensive, analysis. The ideal mesh is usually non-uniform. It is finer in areas where there are large variations in the fluid flow and coarser in areas where variations are small.

    Post-processing provides the means for viewing the results of the CFD analysis. Examples of state-of-the-art interactive graphics tools provided by the latest software include: isosurfaces, perspective views, velocity vector and contour plots, colored streamlines, line graphing and a probe for extracting field values.

    Based on CFD analysis, a designer or an engineer can optimize fluid flow patterns or temperature distribution by adjusting either the geometry of the system or the boundary conditions such as inlet velocity/temperature or wall heat flux. The accuracy of CFD analysis, and the amount of time required to achieve it, are highly dependent upon the number of cells in the control volume grid.

    This technology has been used in the aerospace and automotive fields for more than two decades, and has entered the chemical and other manufacturing industries over the last decade. In some of these industries, “Design it right, the first time,” is encouraged and therefore modeling fits in as a virtual lab before building prototypes.

    The following references offer more detailed discussion of the numerical methods of CFD:

    An Introduction to Computational Fluid Dynamics: The Finite Volume Method, by H.K. Versteeg and W. Malalasekera (Wiley and Sons)

    Computational Fluid Dynamics: The Basics with Applications, by John D. Anderson, Jr. (McGraw-Hill)

    The Finite Element Method (Volume 2): Solid and Fluid Mechanics, by O.C. Zienkiewicz and R.L. Taylor (McGraw-Hill)

    Trust Your MOM (and DM and QMOM)The population balance equation can be solved in two fundamentally different ways. They are known as the Discrete Method (DM) and the Method of Moments (MOM). In the Discrete Method, the various crystal sizes are grouped into discrete bins. The number of bins and the particle sizes associated with each bin are decided a priori. The population of particles in each bin is computed by solving the discrete set of population balance equations — one for each bin.The number density of particles in the unit operation, also called the population of particles, can change due to nucleation, growth, aggregation and breakage or any combination of these phenomena throughout the unit operation. The number of bins and the size ratio between adjacent bins controls the accuracy of the calculation. A large number of bins will increase accuracy but also increase the computational effort. An alternate approach is the Method of Moments (MOM). The population balance equation is transformed into a set of equations for moments of the crystal size distribution. The jth length-based moment is defined as follows:

    pm0507_crystallization_mom-equation
    Using this equation any moment can be calculated from the population of particles, n(L,x.t), at a point in space, x, and time, t, by substituting a value for j into the above equation. The 0th moment represents the total number density of particles of all sizes. The 2nd moment is related to the surface area per unit volume of all particles. The 3rd moment is related to the mass density of crystals. The ratio of 1st to the 0th moments defines average crystal size.Clearly, moments contain valuable information about the crystal size distribution. By solving for just a few of these moments and reconstructing them, a reasonable approximation of the crystal size distribution can be made. The advantage of MOM is that it is computationally efficient compared to DM, but it does not provide the crystal size distribution directly.The Quadrature Method of Moments (QMOM) is a variation of MOM. Quadrature is a numerical method used to integrate the moment equation. Instead of solving for several moments of the population as the MOM method does, QMOM solves for a discrete number, N, of weights and sizes of the population and solves for these in stead of the moments. The weights and sizes are used to reconstruct both the 2N moments or the crystal size distribution directly.MOM is useful for simple cases where there is no need for moment closure, e.g. applications involving nucleation and size-independent growth. QMOM is useful for more difficult cases where moment closure is not possible with MOM, such as applications with size dependant growth, breakage and aggregation. Additional reading for population balance methods is found at:1. Ramkrishna, D., Population Balances: Theory and Applications to Particulate Systems in Engineering, Academic Press, 2000, p. 223.2. Marchisio, D. L., R. D. Vigil and R. Bo Fox, "Implementation of the Quadrature Method of Moments in CFD codes for aggregation-breakage problems," Chemical Engineering Science, v58, n15, August 2003. p. 3337-3351.

    MSMPR May Be Less than Ideal

    Population balance methods were introduced to crystallization processes in the early 1960s. With the mixed-suspension mixed-product removal (MSMPR) crystallizer, the primary assumption in solving the population balance equation is a well-mixed steady-state reactor. With this assumption, one can derive analytical expressions for the crystal size distribution under conditions of nucleation, growth and aggregation.

    Due to the elegance of the analytical solutions, the MSMPR has been widely applied in the population balance literature. But there is a drawback: most industrial crystallizations do not have these ideal mixing conditions and are time-dependent in nature and hence the need for combining population balance methods with CFD. For more discussion on this topic, try “Theory of Particulate Processes,” by A.D. Randolph and M.A. Larson (Academic Press).
    About the Author

    Kumar Dhanasekharan | Ph.D.