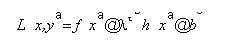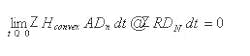Closed System Control: From Defense to Pharma
For pharmaceutical manufacturers, process analytical technology, or PAT, has been the unachievable Holy Grail for almost two decades. The definition sounds simple enough: The Food and Drug Administration (FDA) describes PAT as a framework for designing, analyzing and controlling manufacturing through timely measurements of raw and in-process materials to help ensure desired product quality.
But despite the promise of PAT – primarily, to create an adaptable control process that would allow greater flexibility, innovation and real-time release of drugs – the industry has not widely accepted and deployed the technology. Companies view PAT as untested by precedent, and they struggle with the imprecise guidance language provided by the FDA. As a result, the industry has shied away from implementing PAT, believing the potential for approval delay to be more costly than the expected benefits.
This paper will discuss a proposed process-control design methodology could create a robust and compliant PAT system using established tools developed for the nuclear industry, computer modeling/gaming software, and existing PAT technologies, such as data- and computer-driven chemical analyses.
This methodology mathematically creates a closed system that describes, simulates and provides a completely defensible pharmaceutical-control process. By explicitly incorporating the objectives of PAT into a closed mathematical system, we have addressed PAT semantic uncertainty, thereby paving the way for timely and cost effective PAT implementation.
Introduction
The FDA acknowledges that the drug-approval process is expensive, complex and constrains manufacturing innovation. PAT was developed as an attempt to address this problem. Unfortunately, the goal of the FDA and the prerequisites for PAT appear diametrically opposed. The primary charter of the FDA is to ensure patient safety by reducing risk, while PAT’s flexibility and adaptability objectives require an increase in process degrees of freedom. Since each degree of freedom represents a stochastic variable, implementing PAT must theoretically increase potential process variance.
The concept behind PAT is that sufficient process understanding – coupled with extensive analytical instrumentation and quality-control-measurement procedures – will produce the desired compound repeatedly, reliably and with risk quantification. Certainly on the surface, there is little to argue with this concept.
At the same time, however, the risk-aversion mantra, “you don’t know what you don’t know,” is continually at the forefront of any discussion regarding PAT implementation. Therefore, the potential increase in process variability brought about by the degree of freedom expansion involved with PAT results in a circular argument, and requires negotiation between the FDA and the manufacturer regarding risk management and process knowledge.
This dichotomy between the FDA’s goals and the preconditions of PAT contains an inherent logical fallacy: that the process developer must have perfect knowledge of the process, because the source and implication of any variation must be known a priori. However, if this were true, there’d be no need for PAT.
Proposed approach
To cost-effectively implement PAT, manufacturers require a process control scheme that is adaptive to inherent process variability, but is a mathematically closed system. Such a system ensures that the process always resides within a known, mathematically robust and regulatory-defensible state.
While this may sound impossible, the U.S. Defense Department faced a similar challenge at the dawn of the nuclear age. Control systems for nuclear weapons cannot be subject to the unknown-unknowns. Such a control system must be a mathematically provable system in which every possible state and state transition can be explicitly calculated. The lack of any nuclear-weapons control-system accidents over the past 60 years attests to the success of this design scheme and mathematical proof.
Compared to a nuclear weapon, a chemical or biological synthesis is considerably more difficult, for two reasons. First, the number of variables is substantially higher. Second, most of the variables are stochastic and non-linear, while a nuclear control system is dominated by binary logic.
This complexity has resulted in a lack of exact solutions to the process equations. As a result, control systems have typically been developed through the traditional abstract transfer function approach, which is consistent with pre-PAT concepts. Implementing a PAT control process, in the absence of exact solutions, requires a different approach. We have elected to take a geometric approach and view of chemical and biological processes.
Any chemical or biological reaction can be fully described by a series of partial differential equations. These equations include expressions for items such as rate, entropy, concentration, metabolism, glucose feeding, PH and viscosity – to mention a few of the hundreds of variables that influence the reaction. Adding to the complexity is the fact that many of these equations are nonlinear, recursive and the variables are stochastic.
Simultaneously solving a large number of such equations is not only extremely difficult – it does not converge to a unique solution, making it difficult for control system design.
Mathematical background
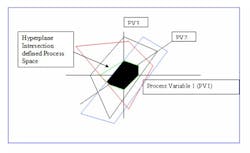
Imagine each variable that influences a reaction as a separate dimension, just as x, y and z represent standard Euclidian three spatial dimensions. A reaction can therefore be projected in N dimensional space, where N is the number of influence variables. We refer to this as the N dimensional Process Space PSn.
We will illustrate the concepts and process using simplified, virtual 3-D graphics because we are limited in print.
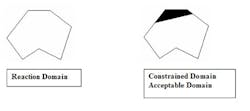
The reaction domain is a closed set, because all possible state vectors are contained within the domain and the result of any operation performed on any process variable is also contained within the domain. Because the reaction domain contains all possible states, some states or geographic regions are undesirable and need to be excluded from consideration. We accomplish this by constraining the reaction domain with additional explicit constraint equations or by applying the Lagrangian method to relevant equations.
The result is an N dimensional closed polygon of acceptable state vectors for the reaction.
The complete space is not convex, but can be decomposed into a series of convex space segments along the time dimension. Consider the space as a Rieman integral: