When the U.S. FDA rewrote its current good manufacturing practices (cGMP’s) for drug products back in 1976, it added the requirement that manufacturers review the quality standards for each drug product every year, and that they write up results in an Annual Product Review (APR). After some manufacturers commented on the proposed regulation, objecting to FDA’s initial report requirements, the Agency revised the proposal to allow each manufacturer to establish its own procedures for evaluating product quality standards. They were to base the final report on records required by cGMPs. The final requirement became law in 1979, as 21 CFR 211.180(e) [1].
Conducted for each commercial product, the APR provides the basis for deciding on steps needed to improve quality. The APR must include all batches of product, whether they were accepted or rejected and/or stability testing performed during the last 12-month period. The APR must cover a one-year period, but does not necessarily have to coincide with the calendar year. A report for the APR addresses the assessment of data, documents and electronic records reviewed.
The data generated from the batch or product are trended using appropriate statistical techniques such as time series plots, control charts and process capability studies. Control limits are established through trending, and specs for both starting materials and finished products are revisited. If any process is found to be out of control, or to have low capability indices, improvement plans and corrective and/or preventive actions must be taken.
Out-of-specification (OOS) regulatory issues have been well understood and documented in the literature [2]. However, out-of-trend (OOT) issues, for product stability, raw materials (RM) and finished products (FP) data identification and investigation are less well understood, but rapidly gaining regulatory interest.
An OOT result in stability, RM or FP is a result that may be within specifications but does not follow the expected trend, either in comparison with historical data of other stability, RM or FP batches respectively, or with respect to previous results collected during a stability study.
The result is not necessarily OOS but does not look like a typical data point. Identifying OOT results is a complicated issue and further research and discussion are helpful.
Regulatory and Business Basis
A review of recent Establishment Inspection Reports (EIRs), FDA Form 483s, and FDA Warning Letters suggests that identifying OOT data is becoming a regulatory issue for marketed products. Several recent recipients of 483’s were asked to develop procedures documenting how OOT data will be identified and investigated.
It is important to distinguish between OOS and OOT results criteria. The FDA issued draft OOS guidance [3] following a 1993 legal ruling from United States v. Barr Laboratories [4]. Much has since been written and presented on the topic of OOS results.
Though FDA’s draft guidance indicates that much of the guidance presented for OOS can be used to examine OOT results, there is no clearly established legal or regulatory basis for requiring the consideration of data that is within specification but does not follow expected trends.
United States v. Barr Laboratories stated that the history of the product must be considered when evaluating the analytical result and deciding on the disposition of the batch. It seems obvious that trend analysis could predict the likelihood of future OOS results.
Avoiding potential issues with marketed product, as well as potential regulatory issues, is a sufficient basis to apply OOT analysis as a best practice in the industry [5]. The extrapolation of OOT should be limited and scientifically justified, just as the use of extrapolation of analytical data is limited in regulatory guidance (ICH, FDA). The identification of an OOT data point only notes that the observation is atypical.
This article discusses the possible statistical approaches and implementation challenges to the identification of OOT results. It is not a detailed proposal but is meant to start a dialogue on this topic, with the aim of achieving more clarity about how to address the identification of out-of-trend results.
This article will focus on studying the OOT trends in finished products and raw materials only. A different approach would be necessary to identify and control OOT in stability, and will be discussed in subsequent articles.
Differences Between OOS and OOT
Out-of-specification (OOS) is the comparison of one result versus a predetermined specification criterion. OOS investigations focus on determining the truth about that one value while out-of-trend (OOT) is the comparison of many historical data values versus time and OOT investigations focus on understanding non-random changes.For example:
The specification limit of an impurity is not more than 0.10%:
Case 1: For a particular batch, the result obtained is 0.11%. This result is out of the specification limit and is called OOS. An investigation is required. Root cause analysis (RCA) is required for OOS investigation. Once a root cause is identified, corrective and preventive measures need to be taken.
Case 2: The result obtained is 0.08%. Although the result is well within the specifications, we should compare the result with the previous batches’ trend. If we find the average value of the trend as 0.05%, then this batch result (0.08%) is called out-of-trend. Any result greater than 0.05% will be atypical results. A systematic root cause analysis is required. After identifying the root cause, we can decide the fate of the batch. OOT is dealt with on a case-by-case approach. A thorough understanding and control of the process is required.
We used the following tools to analyze data in this paper:
- Microsoft Excel
- Minitab
- Crystal Ball
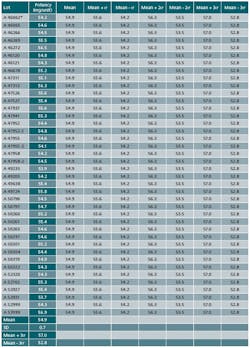
In addition, we used the data set of 40 batches of potency shown as Table 1. The data is amended to satisfy the scope of this article.
Statistical Approach Background
There is a need for an efficient and practical statistical approach to identify OOT results to detect when a batch is not behaving as expected. To judge whether a particular result is OOT, one must first decide what is expected and in particular what data comparisons are appropriate.
Methodology, 3 sigma (3σ):
- Data of 40 batch results has been compiled for fixing the Trend range. A minimum of 25 batches data could be used
- Results of 40 batches are tabulated, mean, minimum and maximum values are established.
- Standard deviation is calculated for these 40 batch results. Excel spread sheet has been used for Standard deviation calculation.
- Standard deviation will be multiplied by 3 to get the 3 sigma (3 σ) value.
- Maximum limit is arrived at by adding the 3 σ value to the mean of 40 batch results.
- Minimum limit is arrived at by subtracting the 3 σ value from the mean of 40 batch results. Minimum value may come in negative also at times.
- The above maximum and minimum limits shall be taken as the Trend range for upper and lower limits.
- Any value that is out of this range will be considered as out-of-trend (OOT) value or outlier value.
- Wherever a specification has only “not more than,” then only maximum limit for a trend can be considered. Minimum limit should be excluded.
- Wherever a specification has range, then both the Maximum and Minimum limits for trend should be considered.
Results and Discussions
Once we arrived at our OOT limits by mean +- 3 σ values, we further authenticated these limits using:
Process Control
To make sure if the process was under control when we established OOT limits, the following charting was done:
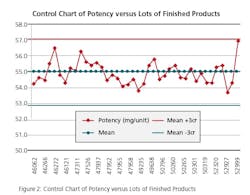
Run Chart: Run charts (often known as line graphs outside the quality management field) display process performance over time. Upward and downward trends, cycles, and large aberrations may be spotted and investigated further. In the run chart (Figure 1), potencies, shown on the y axis, are graphed against batches on the x axis. This run chart clearly indicates that Lot # 52999 with potency value of 56.9 is not an atypical result as it is inside of mean +3 σ value, but is borderline to the 57.0 limit.
This graph indicates that the process is under control but not centered to the mean as per given specifications. The product specifications given by R&D are always subject to update based upon the manufacturing data. Process Capability Indices Cp and CpkCp is the capability index. It measures how well the data fits between the upper and lower specification limits. The higher the value, the better the fit. Cpk is the centering capability index. It measures how well the data is centered between the specification limits. The higher the value, the more centered the data.Thus the Cp and Cpk indices are the primary capability indices. Cp shows whether the distribution can potentially fit inside the specification, while Cpk shows whether the overall average is centrally located. If the overall average is in the center of the specification, the Cp and Cpk values will be the same. If the Cp and Cpk values are different, the overall average is not centrally located. The larger the difference in the values, the more offset the overall average. A process capability study is used to determine whether a process is stable and capable. Process capability indices are used to measure how well the data fits into the specification limits. Frequently used process capability indices include Cp and Cpk. Cp is used to evaluate the variation of the process, and Cpk is used to evaluate the centering of the process.
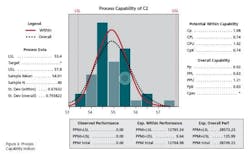
It is important for manufacturers to calculate and analyze the values of Cp and Cpk for their processes and understand the interpretation of such data. It is recommended that the Cp / Cpk values be targeted at 1.33 or above [6]. Process capability studies assist manufacturers in determining if the specifications limits set are appropriate, and also to highlight processes that are not capable. Manufacturers would then be required to take necessary improvement plans / actions.
Calculations of Cp and Cpk for Potency of Given Data
Lower Specification Limit= 53.4
Upper Specification Limit= 57.8
Mean= 54.9
Cp= Upper Specification Limit-Lower Specification limit/6*SD
Cp =(57.8-53.4)/6*0.7
Cp =(4.4/4.2)=1.048
Similarly
Cpk=0.714
Cpk can never exceed Cp, so Cp can be seen as the potential Cpk if the overall average is centrally set. In Figure 4, Cp is 1.048 and Cpk is 0.714. This shows that the distribution can potentially fit within the specification. However, the overall average is currently off center.
This technique has already been used by professionals in fields such as finance, project management, energy, engineering, research and development, insurance, oil & gas, transportation, and the environment.
Monte Carlo simulation performs risk analysis by building models of possible results by substituting a range of values—a probability distribution—for any factor that has inherent uncertainty. It then calculates results over and over, each time using a different set of random values from the probability functions.
In order to analyze OOT data from the APR, a probability distribution function is assigned to the unknown variables, and then Monte Carlo simulations are run to determine the combined effect of multiple variables. The seed value of the individual variables is calculated by the probability density definition of each variable.
A standard sensitivity study shows us the sensitivity of the resulting improvements from the range of outputs from a single variable.
Monte Carlo simulations furnish the decision-maker with a range of possible outcomes and the probabilities that they will occur for any choice of action. Monte Carlo simulations can be run for extremes (either the ‘go for broke’ or ultraconservative approaches) or for middle-of-the-road decisions to show possible consequences.
Depending upon the number of uncertainties and the ranges specified for them, a Monte Carlo simulation could involve thousands or tens of thousands of recalculations before it is complete. Monte Carlo simulation produces distributions of possible outcome values. By using probability distributions, variables can have different probabilities of different outcomes occurring. Probability distributions are a much more realistic way of describing uncertainty in variables of a risk analysis.
Determination of Cp and Cpk Values from Simulations
Simulated Cp= 5.04
Simulated Cpk=4.54
Simulated Cp/Cpk=5.04/4.54
Simulated Cp/Cpk=1.11
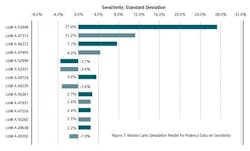
In Figure 5, the ratio of Cp and Cpk of simulations has gone down from 1.47 to 1.11. This gives us an opportunity to look at Sensitivity Analysis to find out the drivers of Risk Analysis. This is an alert to improve our future APR reports. There is also a shift of all our batches to the left to the target values in the simulated model. This is a contrast to the model that we have on Statistical Process Control. The Statistical Process Control model was based upon controls while the simulated model is based upon our specifications. That means that the variability of shifting the model is coming up not only from specifications but from individual lots.
Figure 7 clearly indicates that the drivers of Risk are three lots with lot #s A53999, A47313 and A46272. These lots contribute 27.4%, 11.2% and 7.7% to the variance. The raw materials and production parameters used in these lots should be further investigated to use as a mirror for future years APRs.
LimitationsOne advantage of the Monte Carlo Simulation approach is that, as long as the assumptions are met, the rate of false positives can be set when one calculates the limits. However, a disadvantage is that, when applied to products with limited data, the appropriate limits may be difficult to determine. This can lead to wrongly centered, too narrow, or too wide OOT limits.So far, we have studied trending for Annual Product Reviews using the data of one calendar year. We are in a process of extending the scope of this project for evaluating trending from year to year, which we expect to give us improved process understanding. Our ultimate goal is scoping out the Knowledge Space, and using APR’s to build the Design Space and Control Strategy fundamental to Quality by Design.
References
1. FDA, “Human and Veterinary Drugs, Good Manufacturing Practices and Proposed Exemptions for Certain OTC Products,” Fed. Regist. 43 (190), 45013–45089 (Sept. 29, 1978).
2.Hoinowski, A.M., et al., “Investigation of Out-of-Specification Results,” Pharm. Technol. 26 (1), 40–50 (2002).
3.FDA Guidance Document, Investigating Out of Specification (OOS) Test Results for Pharmaceutical Production (draft).
4.US v. Barr Laboratories, 812 F. Supp. 458 (District Court of New Jersey 1993)
5.Hahn, G., and Meeker, W. Statistical Intervals: A Guide for Practitioners (John Wiley & Sons, New York, 1991).
6.Investigating OOS test results for pharmaceutical production, U.S. Department of Health and Human Services, Food and Drug Administration, Center for Drug Evaluation and Research (CDER), October 2006, Pharmaceutical CGMPs
About the Authors
Bir (Barry) Gujral is Director Quality Engineering and Peter Amanatides is Vice President QA and QC with Noven Pharmaceuticals Inc., Miami, Fl 33186. Mr. Gujral can be reached by email, at [email protected].
Acknowledgments
We sincerely thank Mike Lewis, Director of Validations, and Paul Johnson, Senior Director Analytical Research at Noven Pharmaceuticals Inc for not only reviewing this paper but also for providing their valuable comments. We are also indebted to Joe Jones, VP Corporate Affairs and Jeff Eisenberg, CEO of this company, for their encouragement and kind permission to publish this paper.
