• Magazine
  • ENEWS
  • SUBSCRIBE
  • WEBINARS
  • PODCASTS
  • EBOOKS
    1. Production
    2. Automation & Control

    Demystifying Multivariate Analysis

    Feb. 24, 2005
    In order to identify sources of process variability, you need to be able to integrate information ranging from raw material and intermediate measurements to processing and environmental data. Multivariate analysis techniques such as principle component analysis (PCA) and partial least squares (PLS) can be highly effective. Chris McCready, an engineering specialist with the software firm UMetrics, shows how MVA methods can be applied to improve your process IQ.
    McCreadyFig2
    By Chris McCready, PAT Program Director, UmetricsThe FDA recognized that significant regulatory barriers have inhibited pharmaceutical manufacturers from adopting state-of-the-art manufacturing practices within the pharmaceutical industry. The Agency’s new risk-based approach for Current Good Manufacturing Practices (cGMPs) seeks to address the problem by modernizing the regulation of pharmaceutical manufacturing, to enhance product quality and allow manufacturers to implement continuous improvement, leading to lower production costs.This initiative’s premise is that, if manufacturers demonstrate that they understand their processes, they will reduce the risk of producing bad product. They can then implement improvements within the boundaries of their knowledge without the need for regulatory review and will become a low priority for inspections.The FDA defines process understanding as:
    • identification of critical sources of variability

    • management of this variability by the manufacturing process

    • ability to predict quality attributes, accurately and reliably.
    We must now ask ourselves what methods and tools are available for generation of this process understanding. The analysis method(s) must be capable of integrating the various types of information generated during a full production cycle including
    • raw material measurements
    • processing data from various unit operations
    • intermediate quality measurements
    • environmental data
    These data can then be used to identify which parameters have a critical impact on product quality.Multivariate (MV) methods such as principle component analysis (PCA) and partial least squares (PLS) are ideal for analysis of the various types of data generated from pharmaceutical manufacturing processes.Practical concepts are provided to describe identification of critical sources of variability, calibration of robust and reliable predictive models, application of these models in real-time production and ultimately how the information generated is used for improvement of manufacturing processes.The ChallengeThe greatest hurdle involved in almost any analysis is generation, integration and organization of data. This is particularly true for the pharmaceutical industry, where data are often stored in vast warehouses but rarely, if ever, retrieved.Past regulatory environments did not provide incentives for analysis of manufacturing processes because implementing improvements required revalidation and the current condition of pharmaceutical data infrastructures reflects this.As a result, a great deal of effort is required to assemble meaningful datasets. This challenge is further complicated by the fact that laboratory and production data are usually scattered in various disconnected databases.Since product quality is influenced by all stages of production, including variability of the raw materials, one can only develop process understanding by uncovering the cumulative affect of all processing steps and their interactions. Integrating, synchronizing and aligning data from all relevant sources is therefore a prerequisite before analysis can begin.Assuming datasets are available for analysis, there must be mathematical tools to interpret what the data is telling us. Multivariate techniques including PCA and PLS are efficient methods for visualizing the variability of data, modeling the correlation structure of operational data, calibrating predictive models of quality metrics and identifying critical sources of variability.These MV methods are particularly useful for analysis of production data that contain large numbers of variables of different formats. For instance, production datasets will typically contain a set of raw material measurements, a number of processing steps, intermediate quality measurements and final product quality.The raw, intermediate and final product quality measurements are sampled once per batch and the production processing steps produce a table of time series measurements sampled during production. The complete dataset for a number of batches is shown in Figure 1, where each row in an operating step represents the data generated for each batch.Figure 1 -- A typical pharmaceutical production dataset including raw, in-process and final product quality measurements.
    Review of the types of data generated throughout the complete production cycle of a product yields a new set of challenges. There are a mix of real-time measurements, both univariate (temperature, pressure, pH) and multivariate (NIR or other spectroscopic method), sampled during processing, as well as static data sampled from raw materials, intermediates and finished product.MV methods are an excellent choice for analysis for many reasons. The greatest strength of PCA and PLS methods is their ability to extract information from large, highly correlated sets of data with many variables and relatively few observations. Models generated for prediction of quality attributes also provide information on which of the potentially thousands of variables are most highly correlated with quality. This is an important property for identification of critical parameters.Other strengths include performance on data with significant noise, missing values and the ability to model not only relationships between the X (raw materials and in-process data) and Y space (quality metrics), but also the internal correlational structure of X.The ability to model the internal structure of the X space is of fundamental importance, because a prediction method is only valid within the range of its calibration. Modeling the X space provides a means for recognizing whether a new set of data is similar or different from the training set the model was built on.Thus, MV methods can help predict and justify quality metrics. If the raw materials are dissimilar or a processing unit was operated differently from what the calibration data show, the confidence of the predicted quality metrics must be considered low.The FDA alludes to this point in its definition of process understanding in the PAT guidance as “the accurate and reliable prediction of product quality attributes over the design space established for materials used, process parameters, manufacturing, environmental and other conditions.”The model of the X space contained in these MV modeling methods is essentially a mathematical description of the design space the FDA is referring to in their guidance.Generating Process UnderstandingThe objective in modeling and analysis of this data is to develop process understanding. The FDA provides direction on what it means and how to develop process understanding. The FDA guidance on process analytical technology (PAT) provides four types of tools for generation and application of process understanding including:
    • multivariate tools for design, data acquisition and analysis

    • process analyzers

    • process control tools

    • continuous improvement and knowledge management tools.
    In the FDA’s description, MV methods represent a class of analysis methods, process analyzers are metrics that describe the state of a system, and process-control tools include techniques for monitoring and actively manipulating the process to maintain a desired state.Also included are continuous improvement and knowledge management tools that stress the importance of integrated data collection and analysis procedures throughout the life cycle of a product.  If process understanding is demonstrated through the use of these four PAT tools, the FDA offers less restrictive regulatory approaches to manage change thus providing a pathway for integration of innovative manufacturing methods.Process AnalyzersThe origins of PAT trace back to bringing measurements made in the laboratory into the production environment. PAT was initially interpreted as integrating advanced sensors into manufacturing processes.More recently, however, PAT has grown to mean much more than sensors and so has the concept of a process analyzer. Process analyzers are now portrayed much more broadly as metrics that describe the state of a process.There are many commonly used MV procedures for characterizing the behavior or state of a process. In pharmaceutical manufacturing, unit operations are typically carried out in batches. The trajectory of these batches from initiation to completion can be summarized into a MV signature or fingerprint.Comparison of new batches to this MV fingerprint provides an indication of the state of the process. When the MV trajectory does not match that of in-control batches, the process is behaving abnormally. Shown in Figure 2 is a multivariate representation of a process signature for a single unit operation. The green trajectory represents the average or golden batch, the red lines represent control limits, the blue line displays an abnormal batch progression and the black line represents a good batch.Figure 2 -- Multivariate process signature of a batch process.
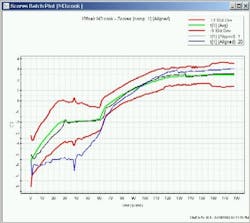
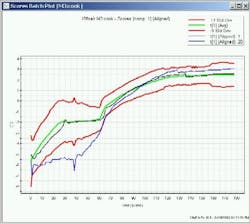
    This MV trajectory is comprised of a weighted linear combination of the underlying raw data at various time points. The weightings are selected to maximize the amount variation described in X.In MV terminology, the value of this weighted linear combination is called a score. Interpretation of the value of the score is an abstract concept in that the connection between the raw data and score is not intuitive. Contributions are provided to describe the variables responsible for a change or deviation in the score. These contributions are very useful in diagnosing the root cause of a process upset and provide a link between the abstract MV scores and the underlying process data.The advantages of using MV process signatures as a process analyzer are many. The risk of the MV trajectory indicating that a batch is progressing normally when an abnormal event has occurred is very slim since scores are typically made up of all underlying process data.If the abnormal event is captured in any of these process measurements, this will be reflected in a deviation of the score. The batch trajectories are very sensitive to changes in the correlational structure of the data and have been found to be very affective for fault detection.A secondary advantage of using the MV process signature for monitoring is the redundancy of information.  Since the score reflects the entire set of process data, no single sensor or measurement is relied upon exclusively.In fact, if a sensor or set of sensors are outputting values that are inconsistent with their typical behavior this will be recognized as a breakdown in the normal correlation structure of the data. Deviations in the correlational structure are captured in a MV statistic representing the constancy of data and are indicative of process upsets and sensor malfunction.Process Control ToolsThe ability to respond to the output of process analyzers and actively manipulate operation to ensure consistent quality is encouraged by the FDA in the PAT guidance. What we are seeing is a shift away from rule-based operational specifications towards maintenance of metrics that are representative of quality.This is significant because if enough information is generated during production to characterize the quality of the material in process, there is no longer a need for intermediate testing of material between processing steps.Typically laboratory testing is used to assure the material has been processed correctly during a unit operation. For example a dryer is run for a predetermined length of time at a set of validated operational settings.When the dryer is finished, the humidity of the material is tested to ensure the drying is complete. If the resulting humidity is within a specified range, the product is released to the next unit operation. If the material is too wet, it is sent back to the dryer for more processing until the humidity is within specifications.The problem with this type of rule-based control is that variations in the material entering the dryer are not consistently managed by the process. If, instead, a process analyzer is used to measure statistics indicative of humidity in real-time, the dryer can be run until a desired endpoint is achieved then released to the next processing step without further analysis. In this way controlling to an end point or other metric representing a quality inherently manages and mitigates variability increasing the consistency of product. It also reduces the need for measurement of product quality between processing reducing production cycle time resulting in improved throughput and equipment utilization.The process signatures described previously are another important process control tool. In this case, the term “process” is used loosely, since it applies to both raw material and production operations. For example, a measurement system may be designed that characterizes raw material quality. If it is recognized that a raw material has a higher water content or particle size, this information may be used as a feed-forward signal to manipulate downstream unit operations to appropriately manage this variability and improve the consistency of the final product.In all cases, the ability to develop process control strategies that affectively manage variability requires:
    • the identification of critical attributes relating to quality

    • sensors that provide information related to these attributes and tools to translate the data generated into meaningful and reliable metrics
    MV methods are affective tools for extraction of information from production data. As described previously, they not provide informative quality metrics but also statistics that confirm the consistency and reliability of data.ReferencesGuidance for Industry, PAT – A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance, U.S. Department of Health and Human Services Food and Drug Administration, September 2004.Pharmaceutical CGMPs for the 21st Century – A Risk Based Approach, Final Report, Department of Health and Human Services U.S. Food and Drug Administration, September 2004.