Keith Melchiors’ article, “Estimating Risk-Based Cost & Contingency” in Pharmaceutical Manufacturing magazine, volume 11, issue 7, is an excellent analytical tool to quantify capital project cost and contingencies. Monte Carlo simulation has been around for a long time, but I don’t think I have ever seen it applied so cleanly and precisely thanks, in part, to the use of spreadsheet technology.
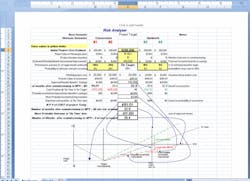
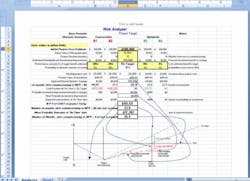
The next logical extension of the project ‘go/no-go’ decision is to apply similar analytical tools to the determination of the financial attractiveness -- breakeven point and net present value (NPV) -- of the project. Estimating the cost is only half of the equation. Estimating the benefit of the investment is the other half. One could adapt Melchiors’ Monte Carlo tool almost directly to the problem of estimating benefit with a statistically calculated level of certainty.However, in the real world, human emotions many times trump analytical tools. The project developer’s hand waving and promises of how great it’s gonna be two, three, four years down the road can foster an unsubstantiated euphoria that leads to a bad decision. Likewise, management’s reluctance to prosecute a project because of some preconceived notions -- such as previous track record of the developer, out of the manager’s comfort zone, not-invented-here syndrome, detraction from other pet projects, etc. -- can kill a perfectly attractive project.The challenge then is to obtain a bias-free consensus on the benefit in the investment that would be realized if the project is implemented. The decision maker, the ‘go/no-go’ person, is human. He/She has opinions and, in fact, was promoted into his/her management position to exert some sage wisdom into decisions. Unless the manager is a mathematician or statistician, a pure, quantitative proposition typically won’t fly. The decision manager needs to emotionally buy into the project and take some ownership for its success.Monte Carlo simulation and random numbers can be too far out of the decision maker’s comfort zone; and, in today’s fast pace world, he/she may not want to take the time to get up to speed on what he/she might consider statistical snake oil. This could make him/her more prone to say ‘no.’ A project has a better chance of success if the manager not only approves it but buys into it. Therefore, as Machiavellian as it may appear, a project developer must convince the ‘go/no-go’ manager within the manager’s aegis that the project should be a ‘go.’In a similar spirit of recognizing uncertainty and statistically quantifying it, I have developed a spreadsheet for assessing benefit that follows much of Melchiors' Monte Carlo methodology, but uses personal inputs from the project developer and the go/no-go manager rather than a random number generator to evaluate different scenarios.Figure 1: Risk Analyzer with base project inputsFigure 1 is a view of the spreadsheet-based tool that facilitates the inputting and evaluation of personal opinion. The yellow shaded cells are the only cells that accept data. Column D is the base project proposal. The project’s agreed-to cost from Melchiors' spreadsheet is entered into cell D6. In the Figure 1 example, it’s $200,000. The estimate of the most likely benefit – derived from either variable cost savings or incremental profit – is provided by the project developer and is entered in cell D9. In the Figure 1 example, it’s $10,000. The cost of money and the duration of the project implementation phase are entered in cell D7 and D8, respectively. These last two data are used to calculate the net present values (NPV) of both the cost and benefits and are used to project the cost of money adjusted breakeven point.Now the fun begins. Like Melchiors' tool, one must recognize that the probability that the estimate is perfect is effectively zero. However, the estimate is somewhere near the middle of the bell curve of all possible outcomes. Melchiors used Monte Carlo simulation to populate the bell curve with hundreds of randomly generated variations and come up with a dollar value for the project’s contingency.The Risk Analyzer shown in Figure 1 is really a negotiating tool for the project developer to dialogue with the manager to obtain approval and to instill some ownership in the manager for the project. It populates its ‘bell curve’ with only five variations. Five inputs do not constitute a statistically significant sample, but five is a convenient number of scenarios that most people can handle in their minds or on one hand. The ideal project scenario is entered into column D. Then up to four other viable outcomes can be loaded into columns B, C, E and F. Each scenario requires two data: the speculated outcome (row 10) and probability of its occurrence (row 11). These entries are entered as percentage. For example, a manager may feel that there is a 25% chance that the project benefits are overstated by 20% or the developer may want to have considered that there is a 5% possibility that the benefits are understated by an additional 10% and suppose both agree that there is a 5% possibility that the project could be a complete disaster and yield only 10% (i.e. -90%) of the initial expectations. Figure 2 shows the results of plugging those other negotiated scenarios into the Risk Analyzer.
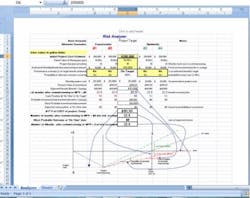
Figure 2: Risk Analyzer with three addition scenarios factored in.Cell D27 displays what is roughly equivalent to Melchiors' contingency value and cell D28 displays the actuality prediction of the breakeven point with all viable scenarios and the time value of money taken into consideration. You will see that the additional scenarios will cause the project to take 2.5 additional months (25.4 – 22.9) to reach the net present value (NPV) point equal zero. The question now for the go/no-go manager is: Is a 25.4 month return an acceptable investment?The significant difference over using Monte Carlo simulation for return on investment assessment is that the decision maker doesn’t need a leap of faith to embrace random numbers. He/she also has input and some ownership in the estimate. This gives the project a better chance at getting the ‘GO.’ The author can be emailed at [email protected].
About the Author
Dan Collins
Dan Collins
Sign up for our eNewsletters
Get the latest news and updates